Mathematics and the real world
By Keith Devlin @profkeithdevlin
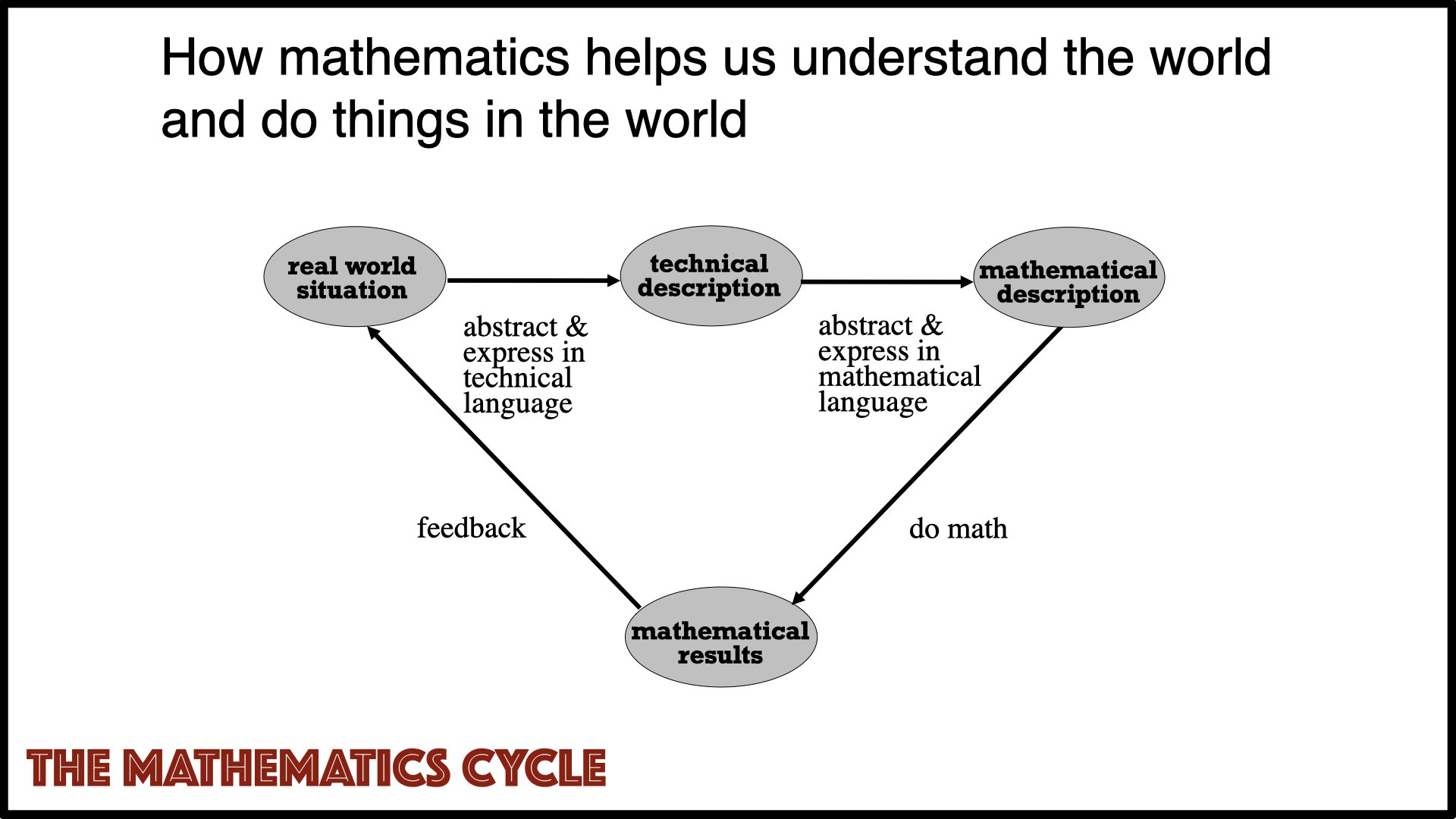
Fig 1. How mathematics connects to our physical or social world. (1) We begin with some real world situation we want to understand or act upon. (2) Using the appropriate domain language, we formulate a technical description or goal. (3) We identify key features in that technical description where we think mathematical precision can help, and formulate those features in mathematical terms. (4) Once we have a mathematical description, we can use mathematical techniques (“do the math”) to derive precise information (i.e., obtain mathematical results that can help us). (5) We then take that precise information and apply it to the original real-world situation, closing the cycle. Sometimes, making progress toward the original real-world goal requires going round the cycle two or more times, each time making more progress.
I’ve been using the illustration in Figure 1 in courses and talks for several decades now. Not only to show how mathematics connects to the “outside world”, but also to illustrate how — and why — new mathematics is developed. (New mathematics may be required if known mathematical frameworks don’t work to get you to Stage 3, or because known mathematical procedures don’t work to get you to Stage 4, or both.)
All professional mathematicians know this picture implicitly, but I’ve never come across anyone else making it explicit in this way. Which I think is a pity, since my experience in teaching and speaking to different audiences is that they never actually saw math laid out “geographically” in this way, and find it illuminating. (I have not put any serious effort into looking for other sources. Since all mathematicians “know it,” it’s very possible others have also made it explicit. There are certainly similar diagrams around talking about mathematical-problem solving, which is related but not exactly the same.)
The two writers who created and produced the hugely successful NUMB3RS prime-time television crime series between 2005 and 2010 (neither of whom is from the STEM world) certainly knew it, since it forms the plot structure for every episode in its six season run. The writers, Cheryl Heuton and Nicolas Falacci, did not get that structure from me; they only knew of me after I had an advance viewing of the series pilot provided by the AMS, and I contacted them offering to assist as a math consultant, which I became for the first three seasons. Like anyone else who studies the way mathematics is used, the Mathematics Cycle (as I call it) picture emerged naturally in their work.
That original pilot episode (based — remarkably closely — on a real case) provides an excellent illustration of how the Mathematics Cycle is used in the world, so let me run with that. See Figure 2.
Fig 2. The Mathematics Cycle forms the plot structure of every episode of all six seasons of the prime-time hit crime series NUMB3RS. This particular illustration is for the Pilot episode that led off the first season. Following the cycle clockwise starting top left: (1) A crime is committed. (2) The FBI is called in to investigate. Agent Don Eppes collects evidence, and formulates an action plan based on well developed FBI procedures. He thinks his younger brother, math professor Charlie Eppes, might be able to help. (3) So Don brings Charlie in as a math consultant. Charlie takes his brother’s police-language description and formulates a mathematical description of what he thinks is the key issue where math might help. In this case, he develops a formula that can lead the FBI to the perpetrator’s home (i.e., he “does the math”). (4) He takes the results of his mathematical analysis and presents them to Don and his colleagues. (5) The FBI team take that information (a probability-contour map showing where the perpetrator most likely lives) and, using the information the map provides, they follow standard police procedures to locate and arrest the perpetrator to close the cycle. [The image top-left of this old slide shows me with NUMB3RS star David Krumholtz, who played Charlie, at a CMC^3 meeting in Monterey in 2007, where we did a joint plenary presentation.]
A couple of comments are probably worth mentioning. Some of the early episodes of the series were based on real cases. The majority, however, were fictitious, but the writers and producers took great efforts to make sure the mathematics presented was correct, and that its use in police work as depicted in the story was mathematically plausible. I was one of a number of mathematicians who assisted in this way, and whenever possible, the lead math advisor Gary Lorden (then Chair of Mathematics at Caltech, where the university scenes with Charlie were filmed) was on set when they recorded mathematics segments.
The Pilot episode actually followed (very closely) a real case, in Lafayette, Louisiana. (The series was located and recorded in Los Angeles, with the Caltech campus used for college location shooting, though for legal reasons it was given a fictitious name.) The math formula shown in the image is the actual one developed to locate the perpetrator (and lead to his capture in both real life and the Pilot episode). It is based on formulating in mathematical terms, studies of the behavior of serial killers. (i.e., The Stage 2 expertise was psychological behavioral studies of psychopathic serial killers.) The computer image shown in the “do the math” part of the cycle leading to Stage 4 is a rendering of the way the original, real-life “Charlie” (a math-savvy policeman from Canada) explained how his method worked. Watch the episode if you want to know more about that part. And if you want to learn about the real case and delve into the real math the Pilot (and other episodes) was based on, see the NUMB3RS companion book I co-wrote with lead advisor Lorden.
With the Mathematics Cycle in front of us now, illustrating how mathematics is intimately and integrally bound up with the physical and social world we live in, let me turn to my main theme. Because the connection of math to the rest of life has recently become a hot item of debate in the United States education world.
“math is about getting the right answer”
Actually there are two issues of contention. One is “What is mathematics?” That’s a legitimate question for the mathematical community to address, and the answer has changed over the centuries, but it has recently been raised by non-mathematicians, and as a result has grown really weird over the past few months. The other question currently being debated is, “How should math be taught in K-12 schools?” In my view, this question should always be under debate. (The same debates have been going on in the UK, by the way.)
For the first question, a number of American states have recently passed or proposed laws that set out to restrict mathematics education to mastery of the procedural mechanics, devoid of any connection to the outside world. “Math is about getting the right answer,” proclaimed one State governor, who was by no means alone in expressing such a view. Views of that nature are, as MAA readers are fully aware, simply uninformed, and students educated in a system that adopts such a view will be seriously unprepared for life in today’s world. [It may be that the two figures I displayed above are technically prohibited in some states. And no, I am not being ironic. I said it’s gotten weird.] But this is not the debate I want to focus on here.
Turning to the second question (the first question will find its way back into the discussion, though not the weird part), states such as my own (California) that value mathematics education more highly (in large part because their economies require a workforce with modern skills), usually leave it to panels of domain experts to develop educational goals and practices, and make policies based on what those panels tell them. Such panels typically seek public input, and that can lead to significant debate. That’s part of the process.
To be sure, some of the input that comes in is ill-informed. For some reason, people who would not claim expertise in piloting an airplane based on having been a passenger in one, or who would not think they could practice medicine based on having been a hospital patient, often exhibit a tendency to think their experience going through the school system makes them knowledgeable about education. It doesn’t.
But that does not mean such individuals cannot provide valuable input to the development of new educational guidelines. Laypersons may not have expert knowledge about how to structure and support learning, but, depending on their particular expertise, they may be able provide input to the process. This is why the development of educational guidelines in the more informed states usually includes procedures for citizen input (which, as far as I can ascertain, is always listened to).
For instance, as a mathematician with decades of experience (in both pure mathematics research and in the use of mathematics in various walks of life), plus my experience teaching mathematics at university level, I can, and occasionally do, provide such input. But I don’t have practical experience in K-12 math teaching or in doing a lot of research on that topic (I’ve done some), anything I say is (I assume) viewed by the experts with that caveat in mind.
In a similar vein, engineers, medical professionals, business people, and numerous others can provide valuable input. In such cases, professional mathematicians like myself are sometimes brought into the development process to advise on how to take account of input from the different sources — all of whom have a valid claim to be stakeholders in the state’s education system.
Once you filter out input from the hopelessly uninformed “math is just about getting right answers” brigade, there is usually something of value to be gained from looking at input from any informed individual, regardless of their domain(s) of expertise. And when you do, you find things can rapidly become more nuanced.
I alluded, somewhat indirectly, to that citizen-feedback part of the educational-reform process in last month’s column, where I discussed the development of the new California Mathematics Framework for the State’s K-12 education system. In today’s essay, I want to focus on just one particular aspect of mathematics education where there is a significant, informed (and for the most part well-intentioned) divergence of views.
Namely, is it the job of K-12 mathematics education to concentrate exclusively on what I will call the “under-the-hood, nuts-and-bolts,” procedural side to mathematics, or should attention also be paid to the way mathematics impacts, and is impacted by, society?
There is a substantial body of opinion within the mathematics education community (K-12 and college level) that K-12 math education should focus exclusively on the inner mechanics of the subject, separated off from any context. (For instance, the educational context that can be addressed by social and emotional learning, a framework developed in the 1960s at Yale School of Medicine as a response to the observation that children from poor economic backgrounds typically perform badly in schools. I’ll come back to this.)
[ASIDE: I note in passing that I was taught math that highly focused, context-free way, and though I was bored by it until I got to high school, and only became excited when I met calculus at age 16, once that excitement was aroused, I pursued abstract pure mathematics with a passion for over two decades, having no interest whatsoever in connections to the outside worlds (physical and social). So it worked fine for me. But as a future professional mathematician, I was not remotely an average K-12 student. And after a few years teaching undergraduate math at large state universities in a number of countries, I learned that most students do much better if provided with some contextual motivation, i.e., if we provide answers to their (sometime unspoken) questions “What’s it all about?” “What’s the point?” and “Why does anyone do this?” ]
Fig 3. Mathematical modeling and its relation to the Mathematics Cycle.
I will say that, for some math topics, that “walled-off, context-free” approach is, in my view, by far the most efficient way to teach and learn. Indeed, at both high school and university level (not K-8), entire courses may be best taught that way. (I am thinking of sharply focused courses like linear algebra, group theory, differential equations, and so on, where the goal is to acquire specific math skills. Though even there, attention should be given to how the course is designed and conducted for the student cohort in the classroom. That’s just good teaching practice.)
The narrow approach is not the way to go with courses for non-majors aiming to develop general mathematical skills and knowledge. [And up through undergraduate level, an entire mathematics education comprising context-free instruction would be educationally disastrous.]
To be a bit more precise about what I mean by “walled off” here, and when and why I think a walled-off approach is best, I need to look again at the Mathematics Cycle, annotated as in Figure 3 to show what is usually referred to as “mathematical modeling.”
A mathematical model arises when the cycle has been followed to the point where there is a precisely defined mathematical description in Stage 3 (often an equation or a system of equations) of some feature of the original real-world domain situation, and the focus then is on “doing the math” to get to Stage 3.
Working with a mathematical model is where you find the kind of activity laypersons typically believe is the totality of mathematics: namely, perform calculations, solve equations, evaluate formulas, and so on.
Once a mathematical model has been created, it’s possible for a mathematician to spend all their time just “doing math”. Yes, in the context of the Mathematical Cycle, there is a clear input, where the model was created, and a clear target for the output. But only rarely does the mathematician have to think about those connections to any great extent.
That approach doesn’t always work, however. You sometimes do have to step back and take another look at the original real-world situation, how it led to the model, and how your results might feed back more effectively into the original situation. (Caltech’s Richard Feynman, officially a physicist, was famous for being able to do that to great effect. NUMB3RS creators Heuton and Falacci told me once that they viewed their world famous Pasadena neighbor as something of an intellectual inspiration.) But most of the time, those connections play no role in many mathematicians’ daily activity.
Going back to education, in the case of a “walled-off” course, those input and output connections provide an excellent (and accurate) answer to students’ inevitable “Why are we doing this?” questions.
In my own case, as I’ve written about elsewhere on many occasions, it was my high-school interest in physics that motivated me to put in the effort to try to master calculus, and thence go on to become a mathematician. For me, the key, motivating “real-world situation” was physics, specifically the emerging field of space flight in the early 1960s. As a university instructor from 1972 onwards, I always taught math-major courses the mathematical modeling way: Start with a brief, and hopefully motivating, session showing how the model of interest arose (the model in this case could be linear algebra, group theory, field theory, differential equations, etc.) and give a nod to existing and potential applications, and spend the rest of the course “inside the walls”, “doing the math.” [Again, with the course designed and conducted for the students I was teaching.]
[Notice, by the way, that the originating “real world situation” for the Mathematics Cycle can be another academic discipline; physics in my case. It can even be an existing branch of mathematics; indeed, that’s how new branches of mathematics often arise.]
It was with university courses for non-math-majors, and in particular non-science-majors, that I learned early in my professorial career that the course would go much better if I spent far more time looking at the entire mathematics cycle (for the course topic). Which is what I increasingly did in such courses.
Recognizing that for most people, the word “mathematics” means the symbols-heavy, procedural stuff, I started to use the term “mathematical thinking” to refer to mathematics pursued with attention to the entire Mathematics Cycle. It’s how I designed and taught my online course (MOOC) Introduction to Mathematical Thinking, offered on Coursera since 2012, and why it has the title it does. [The course is still going strong, and regularly ranks among the most popular math courses on the platform, so there’s definitely a receptive audience for such an approach. It seems to resonate in particular with adult students from the world of engineering.]
And surely, the same mathematical thinking approach will work for K-12 teaching. There is education value in keeping things grounded in the real world we are all familiar with. [K-12 experts I mix with seem in agreement with this, but extrapolating from my experience at college-level teaching to K-12 is the point where I have to flag my lack of any serious K-12 teaching experience.]
Notice that engaging in mathematical thinking (i.e., going around the Mathematics Cycle) involves choices. Much of the complexity that comes with the Stage 1 (real) real-world (be it the physical real world or the social real world) has perforce to be ignored in order to get to Stage 2, and still more has to be discarded to get to Stage 3 (where the “do the math” stuff takes over). That’s a lot of judgements. Who makes them?
Well, you need an experienced mathematician involved in getting to Stage 3, but almost always working in collaboration with a Stage 2 expert. (A lot of the screen time in NUMB3RS focuses on that particular interaction — FBI agent Don for Stage 2 and math prof Charlie for Stage 3.) It’s hard. I know that first hand; I’ve spent the second half of my career working with the Mathematics Cycle framework in different problem domains. In each project, I found myself collaborating with Stage 2 experts from different disciplines, including psychologists, linguists, philosophers, sociologists, and a sociolinguist ethnographer for one very fruitful multi-year collaboration. The upside was a series of fascinating roller-coaster rides where I was the expert in mathematics (the Stage 3 subject) and simultaneously the student of my collaborator in the Stage 2 subject.
“If there is not a constant, heated debate about what math is and how we teach it, we’re doing it wrong.”
Time to switch back to the nuance in the current (non-crazy) debates about proposed developments in K-12 math teaching. One way to view those developments is as attempts to expand mathematics by making broader choices in going from Stage 1 to Stage 2. As I discussed in my two previous posts, both PISA and the California Department of Education have been looking to see how we can modify K-12 math education (including assessment) to better match the needs of the modern world. Both PISA2022 and the new CMF report advocate allowing more contextual features from the social (real-) world to pass to Stage 2, and then find their way to Stage 3. In other words, both organizations have indicated that they recognize the need to allow other contextual factors to find their way into the math class.
Much of the more heated debate focuses on exactly what those new contextual factors are. For instance, Social and Emotional Learning, mentioned earlier. The name turns out to be something of a red flag to many laypersons, so let me mention that SEL-related contextual issues played a huge role in research I did on intelligence analysis for the National Security Agency, the US Navy, and the US Army, following the September 11, 2001 attacks. If you want to look for patterns to analyze mathematically in order to better understand what makes people kill themselves along with thousands of others in a fiery explosion, and find ways to predict and prevent such actions, you’d better go beyond thinking humans are clockwork-like creatures you can apply linear algebra to. Take a look at some of the early episodes of NUMB3RS, including the Pilot, for other reality-based examples.
Some opponents of the changes the CMF team (and other state initiatives) are recommending assert that the proposed new contextual factors do not belong in “mathematics.” That’s really just a matter of definition. The consensus among the mathematical community as to what constitutes accepted “mathematics” has changed many times over the centuries, with new developments sometimes strongly resisted by the existing establishment before eventually gaining acceptance. Time will tell where new disciplinary boundaries fall. The important issue for K-12 education is, what skillsets do tomorrow’s citizens require for their lives?
[Incorporating new contextual factors can of course be legitimately considered as part of mathematical thinking, since making Stage 1 to Stage 2 choices is part of that process. Introducing a new term, like “mathematical thinking,” is just a way to kick the definitional can down the road and get on with what’s needed now.]
The Mathematics Cycle is just a way to picture (simplistically) what actually happens when we humans try to achieve greater precision — in one particular direction — in our thinking. The choices we make in going from Stage 1 to Stage 2 (including what kinds of issues should be brought into Stage 2) are of necessity guided by what we judge to be possible for Stage 3. That means the existing mathematical community always exerts considerable influence. It has to be that way (since it requires considerable mathematics knowledge and expertise), but it carries a risk of getting stuck in a tunnel while the world changes outside the tunnel-walls. To avoid that, we should continually strive to identify and assess the choices that have been made, who made them, and with what purpose in mind. If there is not a constant, heated debate about what math is and how we teach it, we’re doing it wrong.