How can we picture information? How can we model it mathematically? Part I
By Keith Devlin @profkeithdevlin
This month’s essay continues a thread commenced with the May and June posts.
In 1958, Harold (Hal) Leavitt (1922–2007), a managerial psychologist, and Thomas Whisler (1920–2006), professor of industrial relations, both at the University of Chicago, published what would prove to be a highly influential article in the Harvard Business Review titled Management in the 1980s. In that article, they introduced a new term: “information technology.”
They needed a new term because recent, rapid developments of electronic technologies had brought a revolution in the way people executed their daily work and communicated with one another. The authors defined several different types of IT (as it rapidly became known):
Techniques for the fast processing of information
The use of statistical and mathematical models for decision-making
The “simulation of higher-order thinking through computer programs.”
“While many aspects of this technology are uncertain, it seems clear that it will move into the managerial scene rapidly, with definite and far-reaching impact on managerial organization,” they wrote.
A few months later, journalists started referring to the present era as “The Information Age.”
We are so familiar with these terms, most people probably assume that the new (information-) technologies were created to more rapidly or more efficiently handle something called “information” that until then had been collected, stored, and processed by hand. Or, in more fanciful words, the messenger carrying “information” on foot or on horseback had been superseded by the Information Superhighway. Expressed thus, it’s an appealing analogy. But it’s wrong. One of the developments the Leavitt and Whisler article tacitly (but not explicitly) observed, was that “information” in the sense they meant was something new; in fact, it was a product of the new information technologies.
To understand the shift in meaning, I find it instructive to ask ourselves what the word meant to Leavitt and Whisler. It should surely be easy. Familiarity with the word “information” in the IT sense leads us to assume we know what it means (in that context). Well, give it a try: What is information? My curiosity (as a mathematician) about that question was aroused when the Macintosh computer came out in 1984.
The Elliott 803 computer, a transistor-based device manufactured by the UK company Elliott Brothers in the 1960s. About 211 machines were built.
Let me back up. As a mathematician, I became interested in computers when they first started to be available in the early 1960s. The first computer I ever wrote a program for was the Elliott 803, which I got access to in my final year in high school in 1965. I wrote the program in the language Algol-60, when I was working as a summer intern for B.P. in my hometown of Hull. The project was to model the production of industrial chemicals from a management perspective. I could not resist a machine that could do, if not math, then at least arithmetic.
But there was more to it than that. The process of writing a program to manipulate the numbers fed into the computer is very algebraic, and involves what the older me would eventually start to call “mathematical thinking.”
The BBC Micro computer was designed and built in the 1980s by Acorn Computers for the BBC’s national Computer Literacy Project. Over 1.5 million units were sold to UK schools and families between 1981 and 1994, when production stopped.
Many years later, in the early 1980s, by which time I was a young Lecturer in Mathematics at the University of Lancaster in England, the elementary school atended by my two young daughters acquired a BBC Micro, and I volunteered to design and write some simple math games for the children to play. I used the programming language Basic that the machine came supplied with. Again, the mathematical nature of programming appealed to me.
A first generation Apple Macintosh computer, introduced in 1984.
Then, in 1984, along came the Mac, and the moment I tried one out, I started asking myself the question “What is information?” Operating a Mac (or a computer with Windows) is a very different mental experience from programming a computer where you enter commands on a keyboard. At the most basic level, the latter resembles algebra, where you write instructions specifying how to do things to entities to produce new entities, whereas with the Mac you open, close, and move things.
Underneath it all, the same things can be made to happen, but the human experience is very different. At a fairly basic level, one involves choreographing actions on things, with the other you directly move things. In the first case, the “things” acted upon are numbers (though the numbers may be codes for words). But what are the canonical “things” you move on a Mac screen?
We know what the engineers at Xerox PARC (and to some extent SRI) had in mind when they designed the early WIMPS (Windows-Icons-Menus-Pointers) computers in the 1970s; from which the Macintosh took its key design features. Those inspired pioneers set out to create office computers to be used by office workers, who at the time spent most of their time handling written documents and files thereof. What would be the abstraction (corresponding to numbers for command-line computers) for a document?
Information offers an irresistible answer. At least I found it irresistible. After all, documents are where we store information, right?
But then, what is that information, and how is it different from a document? Well, you might say, information is whatever you find in a document. I agree. But the question remains, what is the stuff that is “in” a document that we think should be called information; and in what way is it “in” it?
That was the tantalizing question the arrival of the Mac raised for me. Since, at that time, I and everyone else who used computers thought of them as primarily devices to do math (of certain kinds), I felt information should be reified as some sort of mathematical abstraction. But the more I thought about it, the more it seemed to resemble the Cheshire-Cat; the closer I looked at this stuff called information, it seems to disappear before my eyes, leaving only a tantalizing grin.
As a result of my newly emerging obsession, in 1987 I found myself freshly landed in California at the famous and illustrious Stanford University, which, together with Xerox PARC and SRI had recently founded a new interdisciplinary research institute called The Center for the Study of Language and Information (CSLI). Broadly speaking CSLI’s founding mission was to make sense of all the activities going on around Stanford in what had become known as Silicon Valley. One of their driving questions was to develop a mathematically-based theory of information. Following a visit to CSLI in 1986, I received an invitation to spend a year there. In the end, I spent two years there, and never returned to the UK.
[Fittingly, one of my first acts on arrival in Palo Alto was to buy my first Macintosh computer. I’ve used Macs, and Apple devices in general, ever since.]
As a personal aside, many years later, not long after returning to CSLI as Executive Director of CSLI in 2001, I met the famed Jef Raskin, who started the project at Apple that led to the Mac. He came to my office at CSLI to interview me for Wired Magazine (about both a popular book on mathematics I’d written, my CSLI book Logic and Information, and about CSLI in general), which struck me then and still does as being the wrong way round, given the starry-eyed admiration I have always had about that original Mac interface. Even more, he subsequently invited me to his home on the clifftops outside Pacifica, where he showed me around his personal skunkworks – in true Silicon Valley fashion, a garage.]
By the time I arrived at CSLI, the researchers, led by mathematician Jon Barwise and philosopher John Perry, working with a growing, international cadre of linguists and computer scientists and the odd mathematician, including myself. (A mathematician had to be odd to get involved, since it was not at all clear mathematics would play much of a role. And that turned out to be the case.)
Well, mathematics did not end up playing a major role in understanding information the way it does in, say, physics. What was important, however, is mathematical thinking. It was during my time at CSLI (in fact, I have remained a member of the CSLI research community ever since) that my research main focus in mathematics shifted from Abstract Set Theory to what I ended up calling mathematical thinking.
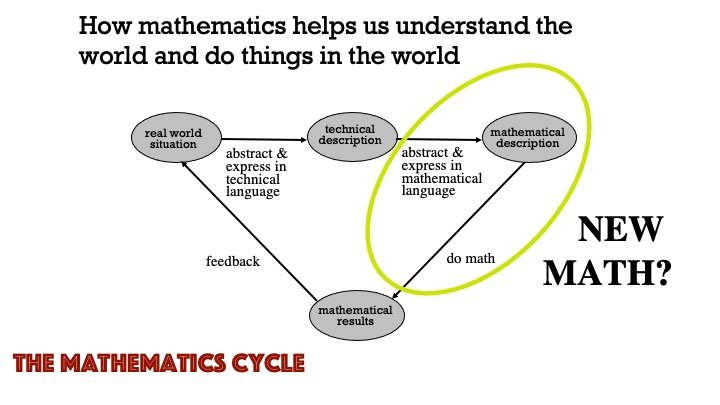
The Mathematics Cycle, which I discussed in last month’s post, came long after the time of my early work at CSLI. Indeed, that CSLI research is one of the drivers that led me to develop that representation of mathematical thinking. Looking back, it captures the way I fitted in to the multi-disciplinary CSLI research community.
We spent many seminar hours discussing how best to model simple “information flow” scenarios where one person would utter a simple declarative sentence to another, and try to understand how the utterance succeeds (when it does) in creating in the listener’s mind a mental state corresponding to that of the speaker with regard to the utterance. And by simple, I mean examples like “It’s raining” or “It will rain.”
So the top left node in the Mathematical Cycle is the two people involved in the speech act (the term linguists use to refer to such scenarios). The linguists in the group would provide a technical description of the act to populate the second node in the formal language of linguistics (syntax, semantics, and so forth). And I’d get into the picture when the mathematical linguists would look at different ways to represent the act (as described technically by the linguists) to try to put something in the top right.
Readers are likely familiar with Chomsky’s groundbreaking work on mathematical syntax; less well known is Montague Semantics. Both frameworks provided ways to populate that third node. My interest, and that of some of the CSLI researchers, including the CSLI leaders Barwise and Perry, was looking for new mathematical frameworks that would better capture the way the speech act works. The two examples I just mentioned captured the language, but said little about the information the utterance conveys. Everyone involved knew some new mathematics was required to do that. That mathematics would have to provide a mathematical model of information (much as the Bohr Atom is a model for the atom).
I’ll describe what we came up with in Part II (next month’s post). The initial idea had been developed by Barwise and Perry (and others) before I arrived. Indeed, it was learning of their approach that led me to make the contact with them that led to my invitation to join the team. (I knew Barwise slightly from our earlier careers in Mathematical Logic.)
Part of developing that “new mathematics” was coming up with a simple picture to visualize a speech act in a way that would guide and drive a mathematical analysis. The equivalent for a new “Theory of Information” of the Bohr atom for Atomic Physics or the Feynman Diagram for particle interactions, both of which I discussed in my last post.
I will begin Part II (of this two-part post) by describing how we went about that, and show you the diagram we ended up with.
Before signing off, however, I should note that the Bell Labs communication engineer Claude Shannon developed a useful mathematical framework that is sometimes referred to as “Shannon’s Theory of Information.” That’s not a good description, given today’s meaning of the word “information” (as I led off with in this post). Shannon himself titled his famous book with Warren Weaver on the subject The Mathematical Theory of Communication. His interest was channel capacity — “How many bits can you get down a wire?” What those bits represented (i.e., the information they carry) was irrelevant. Shannon was working at the level of electrical engineering. The work I am describing here is at the level of human thinking and human-human communication, but done in a mathematical way that makes it practically applicable to human-machine communication and machine-machine communication.
To be continued …